Převozník, vlk, koza a hlávka zelí
Dušan Polanský
Něco málo úvodem
Hned v úvodu upozorňuji, že vůbec nepůjde o to, abychom si namáhali hlavu, natož abychom si navzájem testovali logickou bystrost. Od toho jsou zde jiní, prý povolanější. Hlavolam, který budeme „řešit“, je na internetu nesčetněkrát popsán a vyřešen, tak jaképak copak. Naopak při jeho „řešení“ budeme předpokládat, že se nám jej nedaří vyřešit, a proto se budeme snažit si pomoci tím, že k „řešení“ budeme přistupovat bez jakéhokoliv ostrovtipu, tak trochu nemohoucně. Jedna se o docela známý hlavolam. Začneme jeho zněním.
Hledání řešení hlavolamu
Na levém břehu je převozník (P) s člunem, pak vlk (V), koza (K) a hlávka zelí (Z). Úkolem převozníka je přepravit obě zvířata i hlávku zelí na pravý břeh řeky za podmínky, že se do člunu k převozníkovi vždy vejde buď jenom jedno zvíře, nebo hlávka zelí. Přitom nesmí nechat na břehu spolu samotnou kozu a zelí, protože by nehlídaná koza zelí sežrala, ani spolu nesmí nechat samotné vlka a kozu, protože nehlídaný vlk by sežral kozu. Našim úkolem je poradit převozníkovi, jak to udělat, aby se co nejméně nadřel veslováním.
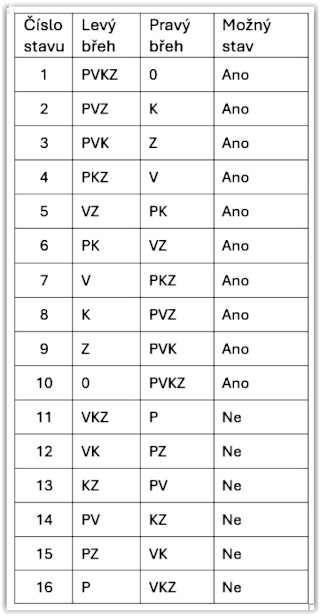
Náš přístup k řešení bude postupně vývojový, abych nepoužil výraz systematický. Nejprve si vypíšeme všechny možné i nemožné situace, které mohou při řešení nastat. Těmto situacím budeme dle úzu říkat stavy. Pochopitelně v dalším nás budou zajímat pouze takové stavy, které splňují podmínky řešení. Příklad možného stavu je, když je na levém břehu PVZ a na pravém K. Příklad nemožného stavu je, když je na levém břehu VK a na pravém PZ, důvod je zřejmý, vlk by sežral kozu. Na obrázku č. 1 jsou uvedené všecky možné i nemožné stavy. Z nich je 10 možných, 6 nemožných. Z možných stavů první je výchozí stav a desátý stav je koncový. Takže k vlastnímu řešení máme k dispozici 8 stavů. Cílem je dostat se ze stavu 1 do stavu 10 při dodržení výše zmíněných podmínek.
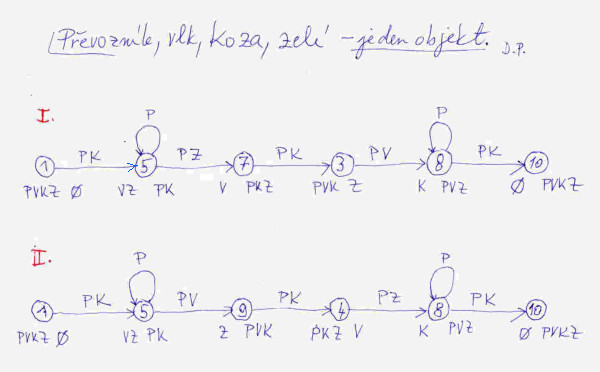
Předtím než začneme hlavolam řešit, je si dobré ujasnit, jak budeme jednotlivé stavy a přechody mezi stavy zakreslovat. Použijeme k tomu zjednodušený stavový diagram ve formě grafu. Příslušný stav zakreslíme kolečkem s číslem stavu uvnitř; čísla budeme brát z naší tabulky stavů. Přechod do jiného stavu vyznačíme orientovanou šipkou. Návrat převozníka na druhý břeh bez nákladu zakreslíme obloučkem nad stavem, po němž se návrat uskuteční. U každého stavu budou zapsány dvě kombinace znaků: kdo nebo co je na levém břehu a kdo nebo co je na břehu pravém. To že, na břehu nikdo není, zapíšeme znakem 0. Klidně si můžete vymyslet jiný způsob zobrazení, kupříkladu ten, že si svisle nakreslite řeku, levý břeh, pravý břeh, a pak postupně vodorovnými šipkami pod sebou to, co právě člun převáží a vše doplníte popisem, kdo nebo co je právě na tom kterém břehu.
Teď stručně k postupu hledání řešení. Vše můžete sledovat na obrázku č. 2. U prvního kroku (tedy při přechodu z počátečního stavu do jiného přípustného stavu) na výběr nemáme; převozník převeze na pravý břeh kozu, tím se ze stavu 1 dostaneme do stavu 5. Pak se převozník vrátí na levý břeh a má na výběr: buď převeze hlávku zelí nebo vlka. Podle toho, jak se rozhodne, dostaneme dvě možná řešení. Při převezení hlávky zelí se dostaneme do stavu 7, při převezení vlka do stavu 9. Další postup je již zřejmý z obrázku č. 2. Vidíme, že při obou řešeních musí převozník převézt člun přes řeku celkem sedmkrát.
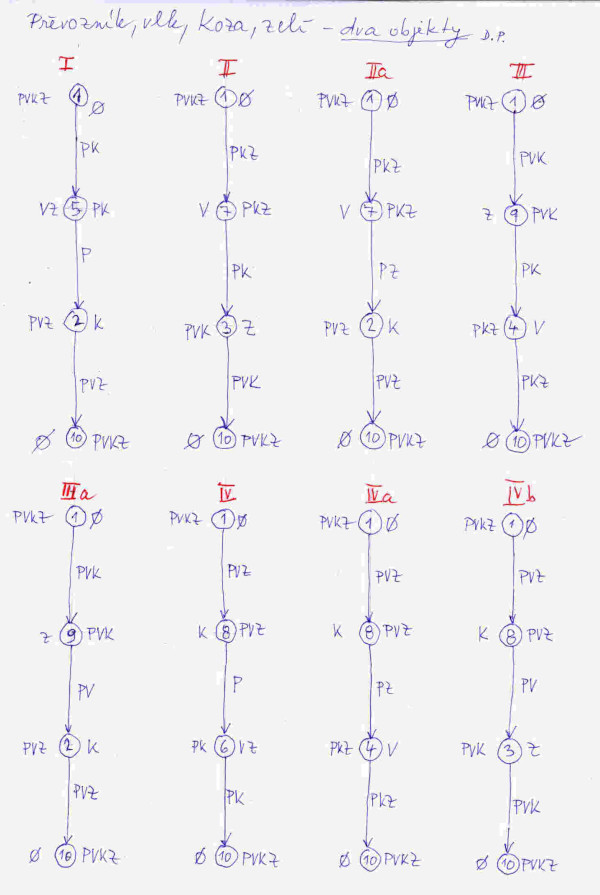
Abychom si tuhle techniku hledání řešení procvičili více, pozměníme trochu naše zadání. Převozník bude moci najednou na člunu převézt dva objekty, tedy buď obě zvířata, nebo vlka a hlávku zelí, anebo kozu a hlávku zelí.
Moje řešení je na obrázku č. 3. Určitě přijdete na to, proč jsem určitá řešení označil stejným římským číslem a malým písmenem podle abecedy. Nejprve začneme řešením, kdy převozník převeze na pravý břeh jenom jeden objekt, pak teprve následují řešení, kdy převozník přepraví na pravý břeh dva objekty. Vidíme, že všech možností je 8 a převozník při každém z nich převeze člun přes řeku celkem třikrát.
Pokud by převozník mohl najednou na člunu převézt tři objekty, stačilo by mu řeku překonat jenom jednou. Ale to by již nebyl žádný hlavolam. Matematici by takové řešení nazvali triviálním
Osobní zkušenost
Dovolím si připomenout, že cílem nebylo vyřešit výše uvedený hlavolam důvtipem, ale ukázat si, že když to nejde takhle, je někdy dobré zvolit si jiný přístup. Uvedu k tomu jednu starší osobní zkušenost. V letech 1978 až 1984 jsem dálkově studoval na VUT v Brně obor elektronické počítače. Důvod mého studia vůbec nesouvisel se zájmem o počítače, což je ale pro tohle povídání zcela sekundární. Specifikem tehdejšího studia tohoto oboru na VUT v Brně bylo, že se poměrně veliká pozornost věnovala výuce překladačů. Ovšem, aby jeden pochopil, jak funguje překladač nějakého programovacího jazyka, musí něco znát z formalizované teorie jazyků a gramatik. Je to sice dost podobné jazykům a gramatice klasických jazyků, ale u těch počítačových je vše striktně definováno a formalizováno. Abych mohl vykonat zkoušku z gramatiky a jazyků, musel jsem mít nejprve zápočet, jenomže abych měl zápočet, musel jsem vyřešit příklad. Jeho přesné znění si již nepamatuji, ale pointa všech příkladů u tohoto předmětu byla stejná. Na vstupu je jakýsi řetězec znaků a ten se má podle určitých gramatických pravidel transformovat do požadovaného výstupního řetězce. Kupříkladu si představme, že na vstupu jsou znaky –+–+–++156. Je potřeba vymyslet taková pravidla, že pomocí nich transformujeme tento řetězec na správný číselný řetězec s jedním aritmetickým znaménkem, buď +, nebo –, v našem příkladu by to dopadlo takto: –156. Pravidla naší gramatiky musí být tak šikovně vymyšlena, abychom jednak uměli načíst číslice, a jednak se zbavili nějak šikovně všech zbytečných znamének a nechali tam nakonec jenom jedno, to správné. Jinak jazyk tohoto příkladu je velice jednoduchý: jsou to číslice 0 až 9 a znaménka +, –. Bohužel příklad se mi nedařilo vyřešit. Co s tím?
V záloze se zdála být poslední možnost, totiž že poprosím některého více inteligentního spolužáka, aby mi příklad vyřešil, za což ho pozvu na jídlo a pivo. Ale nedalo mi to. Šel jsem na to přes grafiku, zkoušel jsem malovat různé grafy; volně, jak mě to napadlo. Nakonec jsem s úlevou zjistil, že můj graf zvládá jakýkoliv vstupní řetězec znaků podle zadání příkladu a vychrlí na výstupu ten správný, požadovaný. Z grafu jsem již snadno odvodil příslušná pravidla gramatiky. Přesto k zápočtu jsem šel s obavou. Po ruce jsem měl kromě pravidel gramatiky i svůj graf. Odborný asistent mi zadal na vstupu vymyšlený řetězec a já měl na svých pravidlech ukázat, že výstup bude takový, jak se dle zadání požaduje. Vše jsem mu vysvětlil na grafu. Byl jsem pochválen, že jsem na to šel přes jakýsi (vyslovil jakési anglicky znějící jméno) automat. Jakýsi píšu proto, že v té době to anglické jméno jsem slyšel poprvé a vůbec jsem jej nepochytil, takže jsem místo odpovědi jenom něco zakoktal.
Na chodbě ukazuje jednomu velice inteligentnímu kolegovi můj graf, a povídám mu, že odborný asistent mi řekl, že to je jakýsi automat. Hned pohotově reaguje: „Jasné, to jsme měli v minulém semestru v logických systémech.“ Tak těm jsem moc nedal. V dálkovém studiu se ve škole celá látka nepřednášela ani zdaleka, většinu látky jsme si museli nastudovat sami. S automaty to bylo možná podobně nebo jsem v té době na přednášce nebyl kvůli časové vytíženosti v zaměstnání. Či tak nebo onak látku kolem automatů jsem zcela vypustil, věříce, že otázku z automatů si nevytáhnu. A opravdu jsem si žádnou takovou nevytáhl. Ale nedalo mi to, hned doma jsme se do skript Logické systémy podíval a zjistil jsem, že je to docela zajímavá teorie. Látku jsem si hned doplnil a znám ji jakž takž dodnes.
Když se nad moji osobní zkušeností zamyslíte, zjistíte, že jsem tehdy postupoval nějak tak, jak jsme zde vyřešili náš hlavolam. Nešlo to důvtipem, tak jsme zvolili jiný přístup, systematičtější. V praxi u složitých problémů se tento přístup používá zcela běžně. Ve své praxi jsem jej použil několikrát.
V Brně 23. dubna 2025.