Kreslíme domeček jedním tahem
Dušan Polanský
Kdo by již od dětství neznal úlohu o nakreslení domečku jedním tahem? Vnučce je osm let a úlohu jsem ji vysvětlil asi před rokem. Domeček nakreslila hravě. Nedávno mi povídá: Dědo, domeček jsme kreslili o přestávce a představ si, že se dá nakreslit různě. Moje odpověď byla nematematická: Asi máš pravdu, vyzkoušíme to. A po příchodu domů a svačině jsme začali zkoušet, při nalezení 11 způsobů nás to přestalo bavit. Ovšem začalo mi vrtat hlavou, kolikaže způsoby vlastně ten zatracený domeček nakreslit. Přiznám se na rovinu, že moje znalosti o grafech (domeček je graf) jsou prabídné. Pouze jsem věděl, že grafům, které lze nakreslit jedním tahem se říká eulerovské. To že musí být souvislý (viz vysvětlení dále) je jasné, ale jak je to s uzly, tedy jaký stupeň (tedy počet hran obsahujících daný vrchol) musí mít?
V Knihovně mám pouze dva tituly, kde je něco o teorii grafů. První je titul [1], který grafům věnuje z 13 kapitol kapitoly 4 až 6. Koupil jsem jej asi před deseti lety, ovšem od té doby jsem na něj nesáhl. A přiznám se, že i teď jsem si z něj přečetl jenom úvod k eulerovským grafům, tedy to, co jsem znal a následně jsem začal v knize listovat, zda tam není uveden vzoreček na určení počtu možností, kterými lze domeček nakreslit. Asi není, jednoduše jsem tam nic takového nenašel, ale budu upřímný, moc jsem se nenamáhal. Knihu jsem opět zasunul do knihovny, ale jsem si slíbil, že se k ní snad někdy vrátím. Druhý titul je [2], autor o grafech pojednává v kapitole šestá, ovšem problematika eulerovských grafů se zde řeší vyloženě okrajově, autor věnuje pozornost jinému problémů. Takže nakonec jsem se rozhodl, že jaképak copak, raději budu rovnou kreslit!
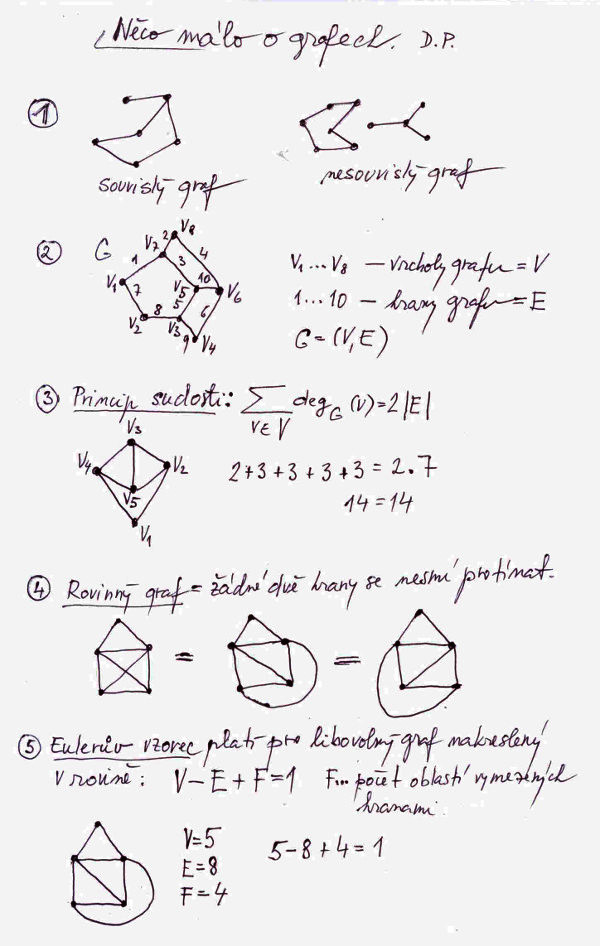
Než se do kreslení dáme, alespoň malé vysvětlení k již zmíněným pojmům; podívejme se na obrázek č. 1. Důležité upozornění: náš domeček bude neorientovaný, tedy můžeme se pohybovat po hranách, jak nás napadne. U orientovaných grafů jenom ve směru orientace hrany. Graf je souvislý tehdy, když pro každé dva jeho vrcholy existuje cesta z jednoho do druhého vrcholu. Graf můžeme zapsat formálně jako G = G(V, E), kde V jsou jeho vrcholy a E jeho hrany. Stupeň vrcholu je počet hran grafu obsahujících daný vrchol, obvykle se značí degG(název vrcholu), přičemž G je název grafu. Známá věta říká, že graf je eulerovský, když je souvislý a každý jeho vrchol má sudý stupeň. Kdyby nebyl souvislý, tak bychom některé vrcholy nemohli spojit cestou, a také je logické, že když do některého vrcholu již jednou vlezeme, musíme se z něj také nějak dostat ven, potažmo opačně, pokud tedy graf chceme nakreslit jedním tahem. Tudíž v případě všech sudých vrcholů žádný problém. Dokonce pak není problém vrátit se do vrcholu, v němž jsme putování začali. Ale bacha, náš domeček nemá všechny vrcholy sudé, dva jsou liché, a to 3. stupně!
Co s tím, když některé uzly jsou liché? Zde nám pomůže historický odkaz na problém procházky po 7 mostech v dnešním Kalinigradu (historicky Královec, Königsberg). Problém byl zdánlivě prostý: projít po všech mostech tak, že nakonec chodec skončí tam, kde začal (na tohle se často zapomíná!), ale nesmí se přitom po žádném mostě projít dvakrát. Nějak to ale nešlo, ať to místní zkoušeli jak jen mohli. Problém vyřešil až švýcarský matematik Leonhard Paul Euler (1707 - 1783) v roce 1736. Dokázal, že projít podobným grafem jako je náš domeček jedním tahem bez opakovaných procházení, je možné jenom v případě, že nebudeme trvat na tom, abychom se vrátili přesně tam, kde jsme začali, a že má méně než tři vrcholy lichého stupně, tedy dva nebo jeden! A to náš domeček splňuje! Má liché vrcholy dva. Ovšem pro jistotu ještě jednou: tahle věta negarantuje, že se vrátíte do výchozího vrcholu. Ovšem k zmíněné větě dodejme, že platí, že pokud máme dva vrcholy liché, tak vždy z jednoho z nich musíme vyrazit a do druhého se vrátit. Zkuste si nakreslit graf, v němž je jeden vrchol lichého stupně a ostatní buď sudé nebo prvního stupně. Lehce poznáte, že i takovýto graf, v souladu s větou Eulera, lze nakreslit jedním tahem, ovšem opět bez návratu do výchozího vrcholu.
Jelikož v našem domečku máme dva vrcholy lichého stupně, můžeme kreslit jednotažky, ovšem bez návratu do výchozího bodu! Vždy v lichém vrcholu začneme a vždy skončíme v druhém. Proč nelze skončit ve výchozím vrcholu lichého stupně. Protože když z takového vrcholu vyrazíme, můžeme se do něj sice vrátit, ale ještě jednou musíme z něj vyjít, abychom prošli i třetí, lichou, hranou. V případě domečku rovněž nelze vyjít a skončit ve vrcholu sudého stupně. Proč? Je sice pravda,že když z vrcholu sudého stupně vyjdeme, můžeme se do něj po projítí všech hran, kromě jedné, té poslední, vrátit, ovšem jaksi je tu problém s vrcholy lichého stupně. Vyzkoušejte si to.
Než se do kreslení dáme, je dobré si uvědomit, že domeček je rovinný graf, jelikož jej můžeme nakreslit tak, že žádné dvě hrany se neprotínají. Na obrázku č. 1 jsem v bodech č. 3 a 5 uvedl dva další zajímavé vztahy z teorie grafů, i když s naší úlohou až tak moc nesouvisí; jenom konstatují určité statické skutečnosti o grafech.
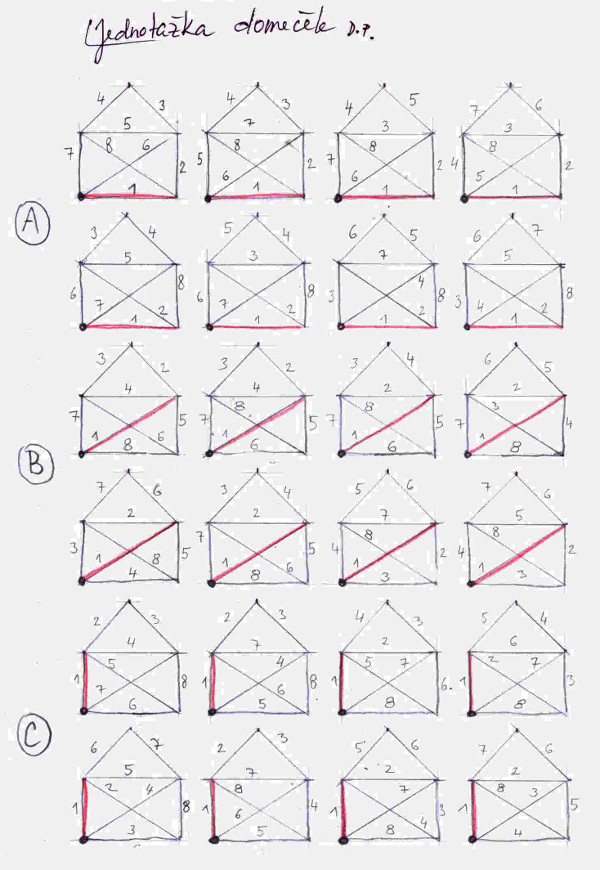
A konečně ke kreslení, viz obrázek č. 2. Vybral jsem si jeden ze dvou vrcholů, který má lichý stupeň a začal jsem vyrábět jednotlivé jednotažky. Jak jsem postupoval, mělo by být zřejmé z obrázku. Červeně jsem pokaždé vyznačil tah, kterým jsem začínal. Vidíte, že jednotažek na obrázku je 24. Pokud bych zvolil druhý vrchol lichého stupně, tak bych stejným způsobem namaloval dalších 24 jednotažek, takže to vypadá na 48 možností, protože když začnete kreslit domeček z vrcholů sudého stupně, domeček se vám jedním tahem nepovede nakreslit. Proč, to jsme si již vysvětlili. V každém případě na tak malý graf je to docela dost možností. A pokud by někdo vzoreček na počet možností nakreslení vykoumal, musel by vzoreček zohlednit vrcholy lichého stupně, protože pouze z těchto vrcholů lze začít jednotažku kreslit. Jinak jsme si již vysvětlili, že kreslení jednotažek vždy končí v lichém vrcholu!
Ono vůbec s grafy jsou jenom problémy právě kvůli bohatosti možností. Možná víte, že za jednu z nejtěžších matematických úloh se považuje problém obchodního cestujícího. Představte si, že jste obchodním cestujícím, který cestuje osobním autem. Někde bydlíte a máte postupně navštívit kupříkladu 40 míst. Je jasné, že chcete ušetřit čas a peníze, takže chcete, aby trasa, kterou urazíte z bydliště (současně je to i místo návratu) byla co nejkratší, přičemž znáte jednotlivé vzdálenosti mezi městy. V teorii grafů bychom řekli, že náš problém je popsán ohodnoceným grafem, jelikož hrany jsou ohodnoceny – v našem případě – kilometry. Vypouštíme složitosti typu, že tahle silnice je v hrozném stavu, a že raději zvolím delší, ale časově rychlejší trasu, prostě všechny silnice jsou v pořádku přesně jako v sci-fi. Z hlediska výpočtu nejde o nic složitého, stačí sečíst kilometry pro každou možnou trasu a pak jednotlivé součty porovnat. Vyhraje nejkratší trasa. Přece máme počítače, nemůže být v tom žádný zádrhel! Ale kdepak je, a parádně pořádný!
Takže kolik je možností pro volbu trasy? Představme si, viz obrázek č. 3, že máme navštívit dvě místa A a B. Možnosti jsou dvě: viz bod č. 1. Teď ať jsou místa tři, tedy A, B, C. Často se uvádí tahle matoucí úvaha, což bude asi tím, že autoři navzájem opisují: při plánování trasy mám tři možnosti, do kterého města vyrazím prvně, když tam jednání skončím, tak mám dvě možnosti, viz příklad s dvěma městy, tedy celkem je 6 možností, jelikož 3 × 2 = 6. Zkuste se ale podívat na obrázku č. 3 na bod č. 2, kde jsem vypsal více než 6 možností, třebaže úmyslně jsem zde uvedl dvě stejné trasy, možnosti č. 5 a č. 8. Z pohledu obchodního cestujícího jsou to totiž de facto stejné trasy, protože se liší jenom směrem jízdy. Zajímavá je možnost č. 3, je označena hvězdičkou, je tak dlouhá, že program by ji již ani nemusel dopočítat, jelikož délka již po čtyřech sčítancích přesahuje zatím dosaženou minimální hodnotu 24. Pokud to ale vezmeme přibližně, můžeme říct, že počet možnosti roste přibližně faktoriálně. Myslím, že výpočet faktoriálu, který značíme ! za číslem, je známý, kupříkladu 3! = 3 × 2 × 1 = 6. Při návštěvě 5 míst možností to již bude přibližně 5!, což je 120. Zkuste si ve vašem počítači zjistit hodnotu 25! Obrovské číslo! A což tak 50! Vidíme, že počet možností roste doslova šíleně, a bohužel v tom je i celý průšvih řešení problému obchodního cestujícího. Zatím nikdo nedošel na to, jak řešení problému zjednodušit. Pokud na to kápnete, přihlaste se v Clayovém matematickém ústavu a bude vám vyplacena odměna 1 milion dolarů.
I když nakonec problém obchodního cestujícího z nás laiků asi nikdo nevyřeší, mezi námi ani matematikům nedávám příliš velikou šanci, nic nám nebrání pobavit děti kreslením jednotažek. A pokud děti domeček zvládnou, zkuste jim vymyslet složitější eulerovský graf, ale pamatujte, že musí být souvislý a kromě vrcholů sudého stupně, těch může být habaděj, liché vrcholy mohou být maximálně 2. A především si uvědomte, že matematika není jenom o výpočtu integrálů či řešení diferenciálních rovnic, ale např. i o kreslení jednotažek. A nepochybujte, že by taková matematika děti nebavila.
Literatura:
[1] Jiří Matoušek, Jaroslav Nešetřil: Kapitoly z diskrétní matematiky, Nakladatelství Karolinum, Univerzita Karlova v Praze, 2007. [2] Kevin Devlin: Jazyk matematiky, Nakladatelství Argo a Dokořán. Praha 2002.
V Brně 18. prosince 2019.